Blog

Georg Bube presented some of these tips and tricks to us in an online seminar, on which this article is also based.

Definition of XC task

An XC task is basically defined by five points, the take-off point, the end point and three turn points (hereinafter referred to as points). The start point (SP) is the take-off, the end point (EP) is the landing and the turn points 1 to 3 are the respective turning points in flight. The theory behind the algorithm used to determine the points is explained below.

A triangular flight is defined as follows:

• Three turning points define the triangular route (turnpoints 1 to 3).
• The distance between the start point and end point is less than 20 % of the total triangular distance.
• The scoring distance is equal to the triangular distance minus the distance between the start point and the end point.
• FAI triangle: The shortest side of the triangle must be at least 28% of the total length of the triangle.

The definition of the triangular flight is identical for the DHV-XC and XContest competitions. It should be noted that the number of points is maximised when defining the task and not the distance. As a result of the different scoring, a flight may be categorised as a flat triangle in the XContest but as a free flight in the DHV-XC.

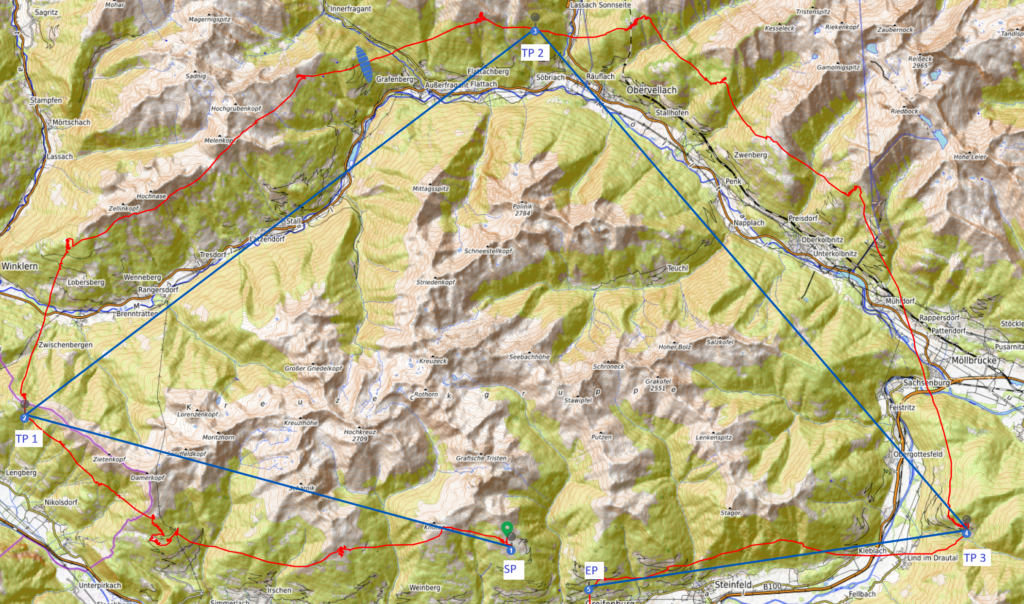
FAI sectors

The figure shows the coloured sectors within which the respective turnpoints 1 to 3 can lie so that the flight is classified as an FAI triangle. The shape of the sectors results from the requirement that one leg must be at least 28% of the total length. If the distance between turnpoints 1 and 3 is constant, turnpoint 2 can be located at any point within the blue sector.

The yellow circle indicates the maximum distance between the start point and the end point for the triangle to be classed as an FAI triangle. The yellow circle is concentric around the start point and has a radius of 20% of the total distance. In order for the flight to be recognised as a triangle, the landing from turnpoint 3 must take place within the yellow circle.

XContest

The scoring on XContest is done according to the rules (see also XContest Rules point 4.2):

• Free flight: free distance that does not correspond to a triangle: 1 km corresponds to 1.00 point.
• Free triangle: Triangle that does not correspond to an FAI triangle definition: 1 km corresponds to 1.20 points.
• FAI triangle: Triangle according to FAI definition: 1 km corresponds to 1.40 points.
• Closed free triangle: Triangle that does not correspond to the FAI triangle definition, with a distance between start point and end point of less than 5 %: 1 km corresponds to 1.40 points.
• Closed FAI triangle: Triangle that corresponds to the FAI definition, with a distance between start point and end point of less than 5 %: 1 km corresponds to 1.60 points.

Example calculation for the Mölltal triangle I flew:

Route length = distance TP 1-TP 2 + distance TP 2-TP 3 + distance TP 1-TP 3 – distance SP-EP
= 25.24 km + 26.11 km + 37.46 km – 3.42 km = 85.38 km.

The shortest leg is 25.24 km, corresponding to 25.24 / 85.38 * 100 % = 29.56 %
The 28 % criterion for the shortest leg of an FAI triangle is therefore fulfilled.

Distance SP-EP to total distance = 3.42/85.38 * 100 % = 4 %
As the distance is less than 5 %, the factor 1.6 is used: 85.38 km * 1.6 = 136.61 points.

I used the Omnicalculator tool to determine the distances between the points using the coordinates. The coordinates of all points can be found on the XContest page under the Route tab.

DHV-XC

Flights are counted as follows for the German Cross-Country Championship (see also DHV-XC FAQ chapter Rating of flights, calculation):

• The distance from the start point around the up to three turnpoints to the end point is always calculated with at least 1.5 points per kilometre.
• For FAI triangular flights (the shortest leg is at least 28% of the total distance), the scoring distance is awarded 2 points per kilometre.
• For all other triangles there are 1.75 points per kilometre.

The scoring rule that results in the highest number of points is applied in each case. The number of points to be awarded for the flight is calculated by rounding the result to hundredths of a point. There is no minimum distance for scoring flights.

Unfortunately, the calculation of the route length and points is not so easy to understand, as the coordinates of the points are not displayed in DHV-XC. I have not checked it, but depending on the programming used to determine the points, there may be different results regarding the coordinates compared to XContest. If you want to know exactly, these points can therefore probably not be used.

The theory behind the calculation of XC points

The XC points are determined by the WGS84 coordinates of the start point, the end point and the turn points. The theory behind determining the points from a given IGC file is quite complex, as the flight route can also be arbitrarily complex. A paragliding flight does not simply consist of flying straight from one point to the next, but is determined by the search for thermals, geographical conditions and airspaces.

Ondrej Palkovsky has described the mathematical theory in detail in his document “Paragliding Competition Tracklog Optimisation”. I had ChatGPT summarise it in a somewhat more comprehensible form:

“The text describes an efficient algorithm for analysing GPS track logs in paragliding competitions. The aim is to automatically find the best possible score from a large number of recorded flight points (often 20,000 to 30,000), for example the longest distance flight, a flat triangle or an FAI triangle. Simple brute force methods would be far too slow for this.

For routes with several turning points (e.g. “free flight” with several legs), a dynamic programming method is used that is significantly faster than trying out all possible point combinations. A so-called branch-and-bound method is used for triangles: the search space is broken down step by step into sub-areas and obviously bad candidates are discarded early on without calculating them completely.

A key trick is the use of bounding rectangles for groups of track log points. With these rectangles, upper and lower bounds for distances can be estimated very quickly without having to calculate each individual point-to-point distance exactly. Although the calculations are made on the spherical surface of the earth, the author shows that the resulting approximations for real paragliding flights cause practically no relevant errors.

Additional optimisations further reduce the computing time, for example by removing unnecessary corner points or detecting almost straight flight sections at an early stage.

The result: even very large track logs can be analysed in seconds to a few minutes, with moderate memory requirements. The approach is therefore well suited for real competition software and shows that precise and fast evaluation is possible even with complex scoring rules.”

The original document by Ondrej Palkovsky can be downloaded here:

Alternative calculation of XC points

Independently of portals such as XContest or DHV-XC, Momtchil Momtchev has implemented his own programming for calculating XC points. He has currently implemented the rules according to FFVL, XContest, XCLeague and FAI. Unfortunately, the DHV XC rules are missing. To calculate the XC points according to different rules, executable files for Linux, Windows and Apple are available for download, or if you have a web server, the programme can also be installed there. Background information and the files are available here. The executable file igc-xc-score.exe offers the following options:

C:\>igc-xc-score
igc-xc-score 1.8.0
Momtchil Momtchev (velivole.fr/meteo.guru) & contributors, © 2020-2024, LGPL 3.0
Usage:
igc-xc-score [in=] [out=flight.json] [maxtime=] [scoring=FFVL|XContest|FAI|XCLeague] [quiet=true] [pipe=true] [progress=] ...
flight.igc is the flight track log
out=flight.json save the optimal solution in GeoJSON format
maxtime=n limit the execution time to n seconds
scoring=FFVL|XContest|FAI|XCLeague select the scoring rules
quiet=true suppress all output
pipe=true read flight data from stdin and write optimal solutions to stdout, works best with quiet
progress= output an intermediate solution every n milliseconds, works best with pipe
hp=true enable High Precision mode (twice slower, precision goes from 10m-20m to 0.6m)
trim=true auto-trim the flight log to its launch and landing points

I calculated the XC points from my Mölltal triangle flight with this tool (output in the Windows command prompt):

C:\>igc-xc-score igc.igc scoring=XContest hp=true
{ in: 'igc.igc', scoring: 'XContest', hp: true }
best so far is Closed FAI Triangle 126.78 points 82.68km ( <147.30 ) 
best so far is Closed FAI Triangle 136.77 points 88.92km ( <137.28 ) 
best so far is Closed FAI Triangle 136.85 points 88.97km ( <137.07 ) 
best so far is Closed FAI Triangle 136.86 points 88.98km ( <136.91 ) 
best so far is Closed FAI Triangle 136.88 points 88.99km ( <136.90 ) 
best so far is Closed FAI Triangle 136.88 points 88.99km ( <136.90 ) 
Launch at fix 0, 09:40:09
Landing at fix n-0 13:35:52
   TP1 : TP2 : 25.29km (25.286km)
   TP2 : TP3 : 26.12km (26.115km)
   TP3 : TP1 : 37.58km (37.576km)
Best solution is optimal Closed FAI Triangle 136.88 points, 88.99km
Multiplier is 1.6 [ closing distance is 3.44km ] [ penalty is 3.44km ]

A comparison of the distances between the points:

	igc-xc-score	XContest
TP 1 to TP 2	25.29 km	25.24 km
TP 2 to TP 3	26.12 km	26.11 km
TP 3 to TP 1	37.58 km	37.46 km

The differences between igc-xc-score and XContest are probably due to the different programming used to determine the points.

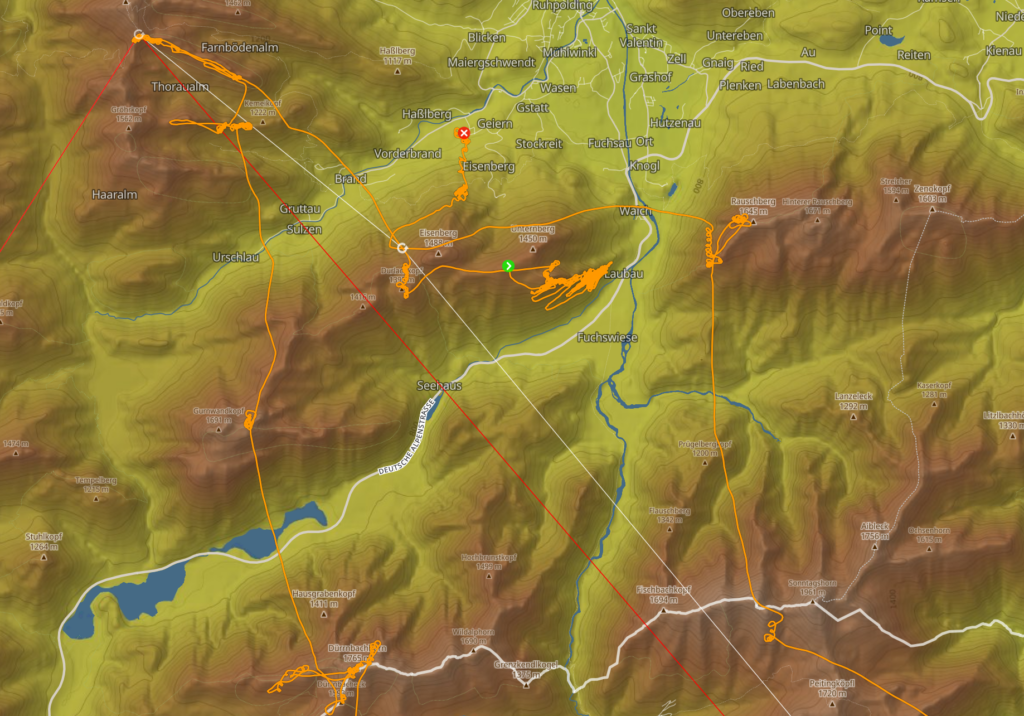
Maximise XC points and average speed

The following option is available for the points hunter to optimise the XC points and the average speed. The average speed is calculated using the evaluated distance, i.e. from the start point to the end point. In Georg’s flight shown below, it did not work as well as hoped at the beginning. The result was a longer soaring flight south of the start point. To prevent the soaring at the start from being included in the average speed, Georg crossed the flight path from the start of the flight after the soaring at the end of the flight (see white ring in the centre of the picture). The start point and the end point, which are included in the calculation of the XC points, have therefore also been redefined. This has the further advantage that the distance between the start point and end point is not deducted when calculating the XC points.

Has this article helped you to understand how XC points are calculated? Perhaps you will be more successful in the future when chasing points in competitions as a result of this article. If you would like to donate as a result, I would give half of the donation to Georg, as his seminar was the main basis for this article. Please indicate in the comment field of the donation that the donation was made because of this article. Thank you very much.